Riptide: Fast, Full Binarization in TVM
Riptide is a new method for quantizing models down to 1 or 2 bits that can enable end-to-end speedups of up to 12X when optimized using TVM. I presented Riptide in March this year at MLSys, but wanted to share why we built Riptide and provide a quick peek into how it works under the hood. Automatic ultra low-bit is a feature we plan on adding to OctoML in the coming year, but until then intrepid machine learners can take a crack at optimizing their models using the open-source Riptide project and details from our MLSys paper.
Motivation and Background
Machine learning is moving fast. Nearly every month a stellar new model considerably advances the state-of-the-art for some new vision or language task. These improvements are often driven in part by new fundamental algorithmic and architectural innovations, but significant advances are also being enabled by the ever-expanding compute and memory available for deep learning tasks.
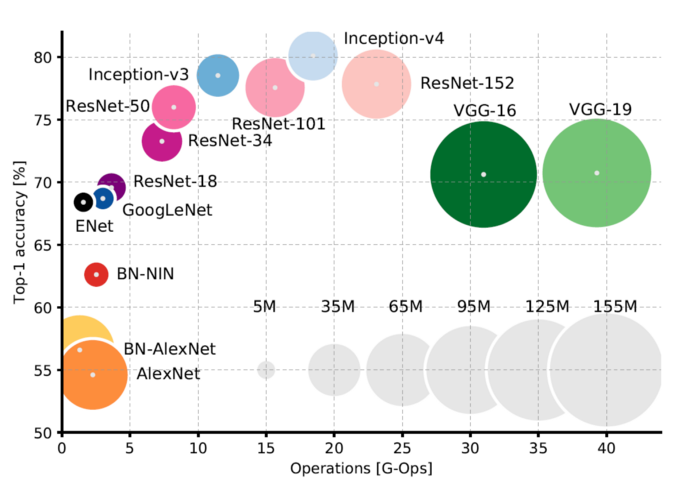
As the ML accuracy frontier advances, so too do computer and memory requirements. Canziani et al. 2016
Even back in 2016, we could already see the trending relationship between model size and accuracy. Today, many state-of-the-art models can only effectively be executed on the latest NVIDIA GPUs (or often a cluster of GPUs). This limits deployment options since many users will not be running a high-end GPU costing thousands of dollars. Application developers may justify such costs for training since a network may only need to be trained once. However, once a model is deployed, it will often be constantly executed by vast numbers of users. To deploy state-of-the-art models at this scale typically requires streaming inputs to the cloud and predictions back down to user devices. While many applications depend on this approach, it has several drawbacks: network connectivity, increased latency, privacy challenges, and substantial, complex infrastructure.
To avoid these drawbacks, many teams are exploring how state-of-the-art models could be executed directly on lower-cost end-user hardware like mobile phones or IoT devices. This is a significant challenge as such devices do not have the compute or memory to directly execute state-of-the-art models designed for cutting edge hardware. For example, a Raspberry Pi 3 is roughly 4000 times slower than an NVIDIA Titan GPU. To adapt high-accuracy models to such platforms, recent research has begun exploring how networks can be adapted to run faster and use less memory. At high level, these techniques follow two strategies: architecture refinement and approximating optimizations. Architecture refinement involves finding new ways of connecting layers to reduce latency or improve parameter efficiency. MobileNet and SqueezeNet are two well-known examples of mobile-focused architectures. In contrast to creating new mobile-friendly models, approximating optimizations seek to make existing models faster by speeding up operations while retaining enough accuracy.
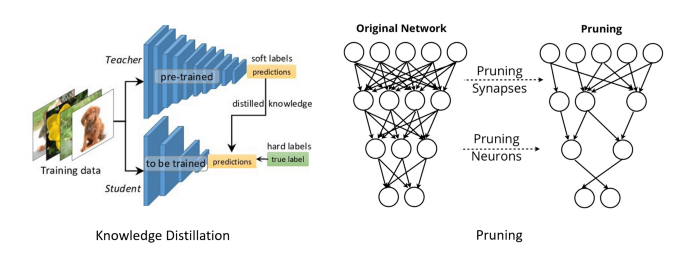
Visualization of two popular approximating optimization. Hinton et al. 2015 (left), Han et al. 2016 (right)
Of the several approximating optimizations which have become popular recently, two representative examples (pictured above) are Knowledge Distillation, which attempts to use a large teacher network to better train a more efficient student, and Network pruning, which removes low-impact weights and activations from a network. In this post, we’ll be focusing on another technique that is particularly interesting due to its generality and significant potential speedups and memory compression benefits: network binarization.
Binary Networks
To improve performance and decrease memory requirements, teams increasingly quantize activations and weights when deploying a model. For example, an engineer may transform model to operate over int8 (8-bit integers) during inference instead of the float32 (IEEE 754 single precision floats) often used during training. Small integer operations are not only faster than floating point arithmetic; because they take fewer bits they can also significantly improve throughput by making the most of the available memory bandwidth. In practice, many models can easily be quantized without losing much accuracy, so this technique has quickly become popular.
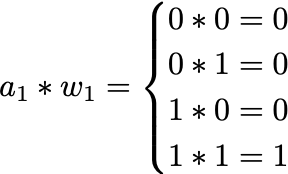
Furthermore, if we consider a bit with value 0 to represent -1 then the truth table becomes that of an XNOR gate.
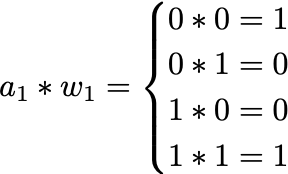
The bitwise gate equivalence of multiplication at 1-bit allows us to replace floating point operations with much more efficient binary operations.

Comparison of a floating point dot product (top) with binary dot product (bottom).
Counting the number of operations in the inner loop of the dot product in the above image shows that binarization can reduce the number of operations in a layer by around 43X and the size of parameters by 32X. When great numbers like these were first reported by Courbarioux et al. in 2016, they kicked off a flood of binary network research. Of course, approximating 32-bit floats with 1-bit values is a lossy approximation. Binary networks typically take a noticeable accuracy hit compared to their corresponding full-precision networks, often around a 20% relative loss of top-1 accuracy. Thus, a major focus of binary network research has been on reducing accuracy loss.
Although works such as Rastegari et al., Cai et al., and Choi et al. make strides towards more accurate binary networks, none of them actually implement the networks in a way that can measure end to end speedups. This lack of implementation not only makes it difficult to know how fast binary networks actually are, it also prevents them from being used for in many practical settings. The reason for the lack of implementation is that if you were to write a simple loop based binary matrix multiply, it would be dramatically slower than most full precision multiplies despite having a lower operation count. A function’s run time isn’t determined purely by its number of operations; the way memory is accessed also plays a huge role. Any binary network implementation must compete against libraries like OpenBLAS and MKLDNN which are hand-optimized by large engineering teams over many years. It’s simply not feasible for most research institutions to devote the amount of time and effort necessary to build a competitive operator library. Instead, they simulate binarization during training and assume speedups are predictable based on operation count.
Riptide
To address these challenges, we present Riptide, an approach to identify and address bottlenecks in end-to-end binary networks. Riptide builds on TVM, a compiler for deep learning systems, which enables us to automatically generate tuned, high-performance binarized operators.
To date, binary network optimizations have narrowly focused on different strategies to efficiently implement core low-bit convolution layers. This focus is motivated by the assumption that binary network performance mirrors the behavior of higher-precision networks: if core convolutions can be made accurate enough using as few bits as possible, then the entire network will be fast. However, no binary networks are composed solely of convolutions; there are many critical intermediate operations between convolutions that are needed to massage data for the next layer. Such layers contribute negligible latency in higher-precision networks, but in binary networks, where convolutions are up to 43X faster, these intermediate “glue layers” become significant.
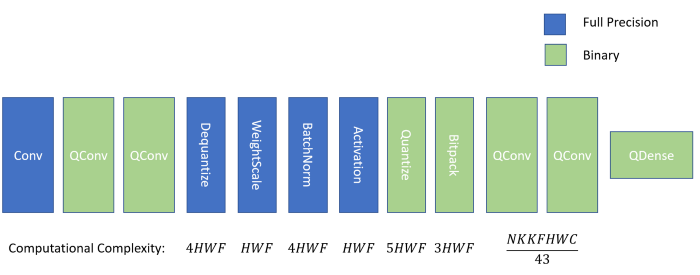
Visualization of glue layers between binary convolutions and their computational complexity. H and W represent input dimensions while F represents the number of filters.
The vast majority of binary networks today include at least the 4 blue layers shown above between QConv and Quantize. From left to right, the output of a quantized convolution (QConv) is first dequantized from its integer form to the equivalent floating point. Next, scaling is applied using weight scaling (which propagates the magnitude of the real valued weights) and then batch normalization (which keeps the distribution of activations predictable). A nonlinear activation such as ReLU is applied and the result is requantized to single bits and packed in preparation of the next quantized convolution.
To understand the impact of glue layers, consider SqueezeNet, one of the more efficient architectures for mobile deployment. Assuming a typical input size of roughly 200x200 pixels and a perfect roofline implementation of binary convolution that runs 43X faster than full precision, we can estimate how much of the total execution time the network spends in the glue layers.
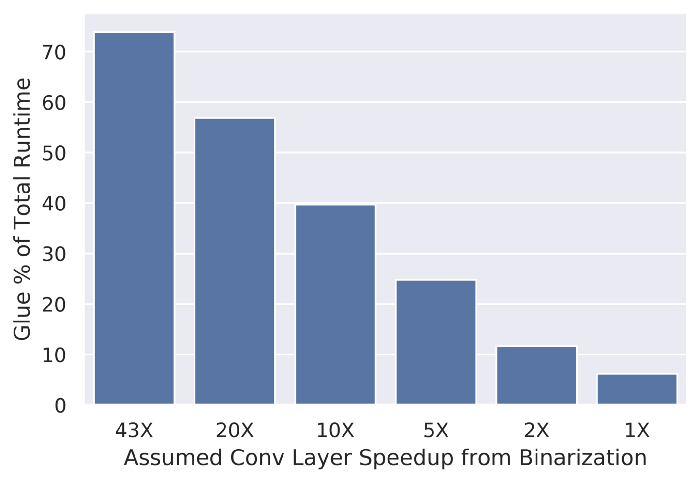
Time spent in glue layers for varying binary convolution speedup.
Assuming binarization yields anywhere near a 43X speedup for convolutions, we can further estimate that higher-precision glue layers will consume about 70% of total inference time. That’s a pretty huge bottleneck! Even at more meager convolution speedups like 20X and 10X, glue layers can still consume roughly half of inference time. We argue that to really exploit the promise of binarization, glue layers must go binary too!
n Riptide, we introduce the fused glue operation, which completely replaces glue layers with just two instructions. The details of how we derive the fused glue operation are a little too gnarly for this post, but definitely check out the paper for more detail if you are curious. Our key idea is to replace multiplications with shift operations by approximating scaling terms to their approximate power of 2 and to replace floating point additions and subtractions with fixed point quantized approximations that can be directly added to binary convolutional outputs. All together, this result in the following set of equations:
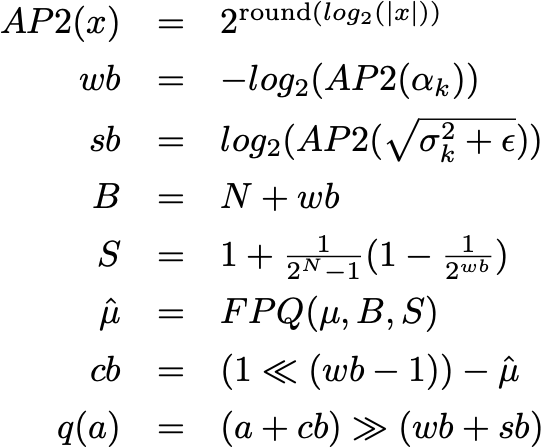
Where N is the number of bits used to quantize the networks activations and the last line solving for q(a) gives the full equation for the fused glue. By substituting this fused glue operation, we can create a Fully Binarized Network:
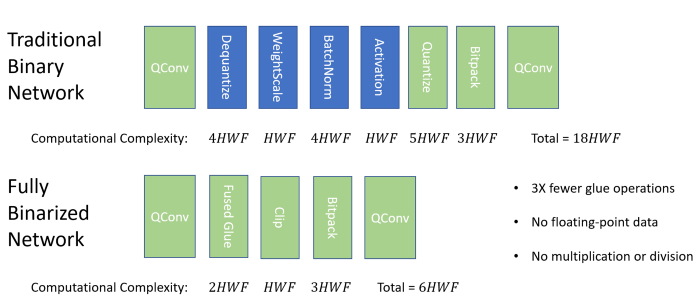
Operation counts in a traditional binary network vs. a Riptide Fully Binarized Network.
We also performed an extensive sweep of accuracy results on the ImageNet dataset and found that our fused glue operation does not cause any accuracy loss relative to other state-of-the-art binary networks. That’s great news because with the glue bottleneck eliminated at an architectural level, we can now drill down into generating fast binary convolutions and measuring end-to-end performance.
End-to-End Speedups
Earlier, we motivated binary networks as an approximation technique to help deploy efficient models for mobile and IoT devices, so let’s see how Riptide performs on the Raspberry Pi 3b. These widely-available and inexpensive Pis are built on an ARM Cortex-A53 processor, which makes them representative of the resource-constrained environments binarization targets.
First, we compare a naive for-loop based implementation of our network to a full precision baseline that uses MKLDNN to accelerate its floating point operations.
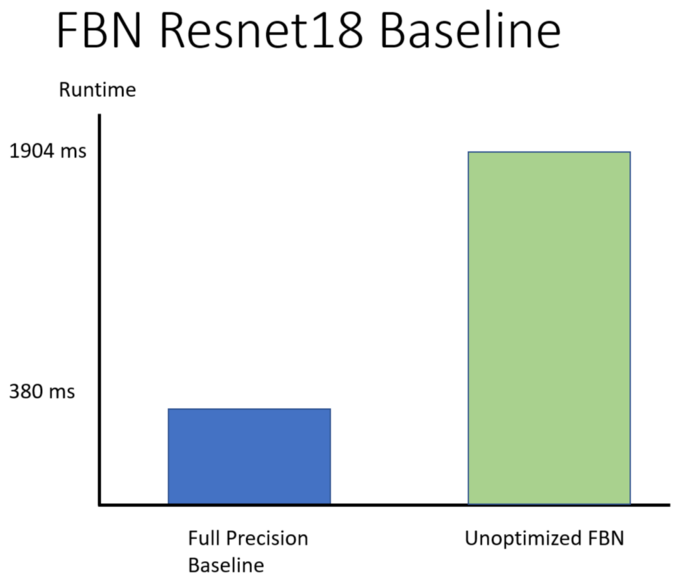
Full precision ResNet18 using MKLDNN run time vs. unoptimized fully binarized network.
Without optimization, we clock a fully binarized network (FBN) version of ResNet18 at roughly 5X slower than the corresponding higher-precision network. To really take advantage of binarization, we also need to generate a well-tuned execution schedule. We get such schedules by implementing binary operators in TVM and leveraging its powerful scheduling and optimization capabilities. In particular, TVM provides the following schedule intrinsics that can be applied to optimize a function:
- Tiling breaks a computation into chunks to improve memory locality of loads.
- Vectorization exploits hardware SIMD instructions for more efficient operation execution.
- Parallelization leverages MIMD facilities such as multiple cores.
- Loop Unrolling replicates the body of a loop to reduce overhead.
We additionally employ the fast popcount operator from Cowan et al. 2018. Finally, we introduce a new optimization called bitpack fusion:
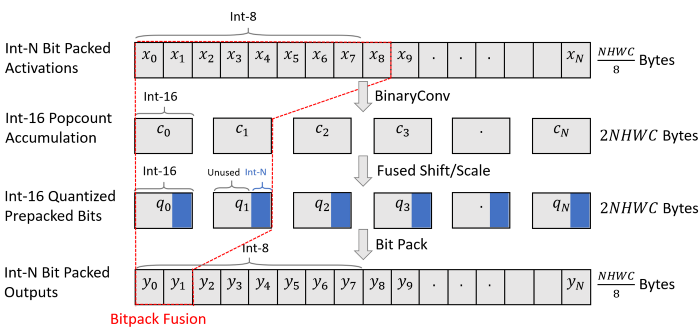
Bitpack fusion folds bitpacking into convolutions to reduce activation memory consumption.
At a high level, bitpack fusion folds bitpacking into the preceding convolutional kernel wherever possible. This can reduce intermediate memory requirements by 16X and enables more efficient copying strategies, providing further speedups.
All together, that’s a bunch of different optimizations. Which ones matter?
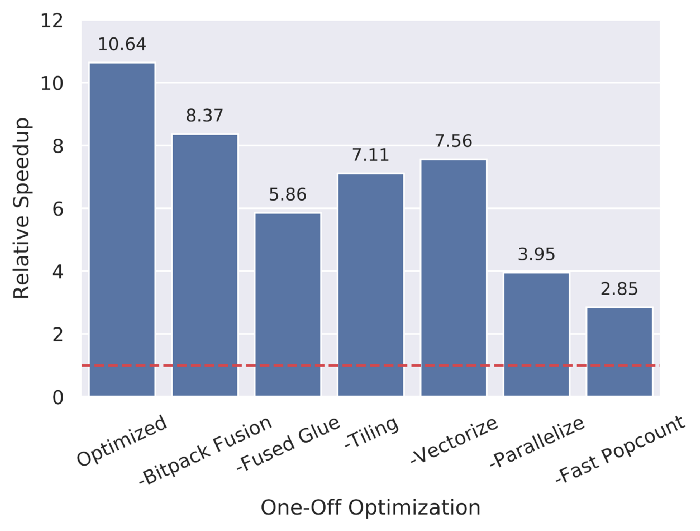
One-off ablation study on FBN speedup from various TVM optimizations.
To answer that question, we performed an ablation study on SqueezeNet as shown above. We found that each optimization significantly impacts speedup versus the higher-precision floating point baseline. When all optimizations are applied together, we see speedups of 10X on real models. While 10X is less than the 43X we might hope for on paper, this order-of-magnitude improvement dramatically expands the range of devices where we can efficiently run state-of-art models. Of course, this speedup is only valuable if Riptide-optimized models can also provide enough accuracy.
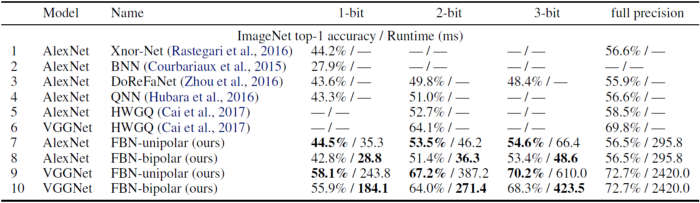
Accuracy and run time results of all Riptide FBN models at various activation bitwidths vs. other state-of-the-art binary networks.
The table above details accuracy and run-time tradeoffs for for several popular binary models at 1, 2, and 3-bit activations. Overall, we found that Riptide FBNs are consistently as or more accurate than other state-of-the-art binarization techniques while providing better speedups: with appropriate activation bitwidth and quantization polarity, FBNs offers speedups between 4X and 12X, making it easy to find one that fits any application’s accuracy needs.
Conclusion
In this post we introduced binary networks and presented Riptide, our method for generating fast end-to-end, ultra-low bit models. Although we haven’t yet hit the hypothetical speedup ceiling, we are already able to generate accurate models with an order of magnitude speedup over higher-precision baselines. If you want to learn more or train and deploy your own binary models, make sure to check out the Riptide paper presented at MLSys 2020. And stay tuned to what’s happening at OctoML by signing up for our mailing list on our homepage, where we’ll making ultra-low bitwidth support for your models even easier through OctoML in the near future.
Related Posts

We introduced support for WASM and WebGPU backends to the Apache TVM deep learning compiler. Our initial experiments shows that TVM’s WebGPU backend can get close to native GPU performance when deploying models in the browser.


Autoscheduling enables higher performance end to end model optimization from TVM, while also enabling users to write custom operators even easier than before.


