Amplify ML Hardware Design Productivity with TVM-driven Hardware Simulation
Authors: Luis Vega, Thierry Moreau
Machine learning (ML) has spurred tremendous innovation in CPU, GPUs and NPUs. But we all know that good software support can make or break the adoption of new hardware. Therefore, it is critical that novel hardware gets co-developed with the compiler that programs it. This co-development is key for making hardware-software design fully agile, adapting quickly to the ever changing trends in ML.
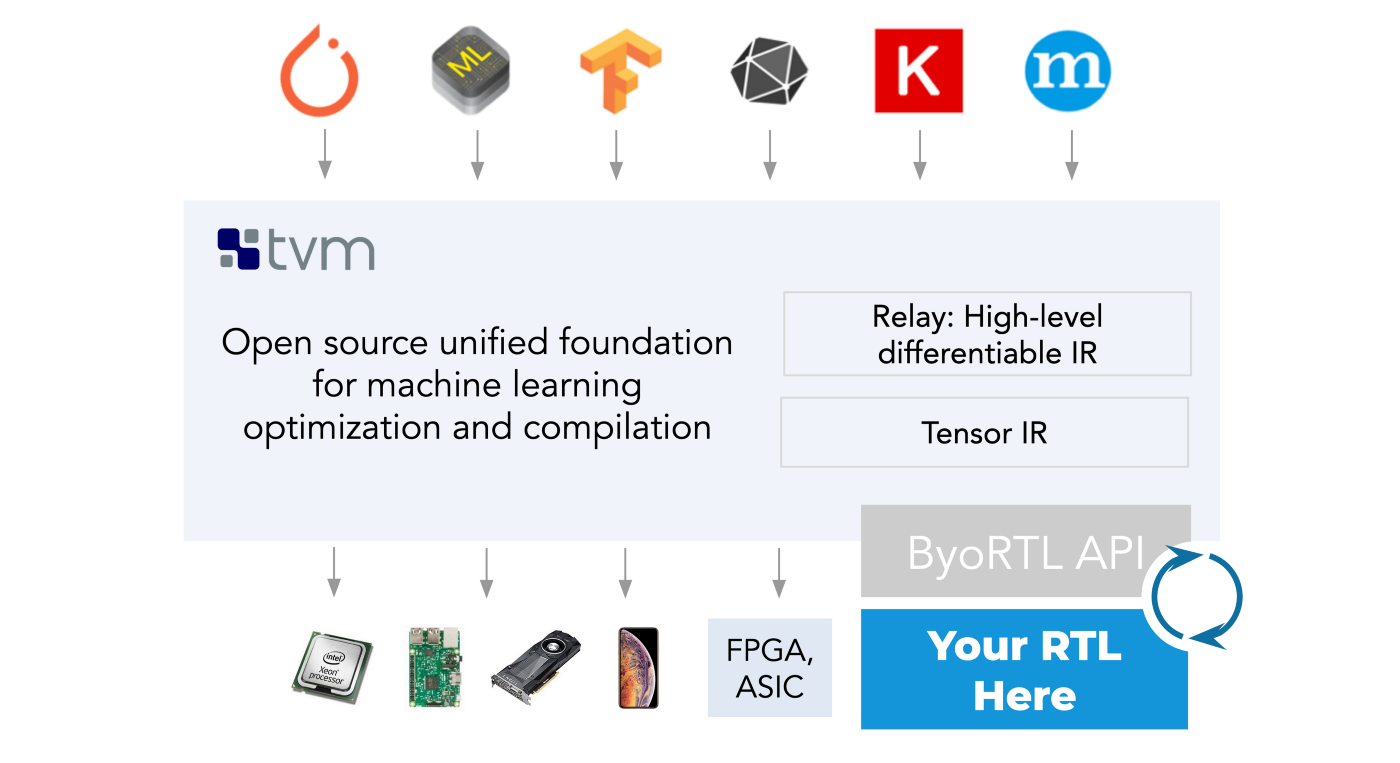
What we propose here is an ergonomic integration mechanism to Apache TVM, the open source ML compilation framework, that allows hardware developers to simulate their designs on real ML workloads from day one. Today, we present the first chapter of a multi-part blogpost series on how to drive simulation from complete ML workloads using this new mechanism in TVM.
Motivation
The methodology used today for evaluating hardware designs is limited to traditional simulation techniques, using low-level hardware tests and micro-benchmarks often decoupled from real-world ML workloads. On the other hand, the integration of these accelerators to ML frameworks will often take place once hardware is manufactured (ASIC) or emulated (FPGA). Independent of the target technology, today’s ML hardware-software systems are generally evaluated on real-world ML workloads once the entire design cycle is completed as shown in the following figure:
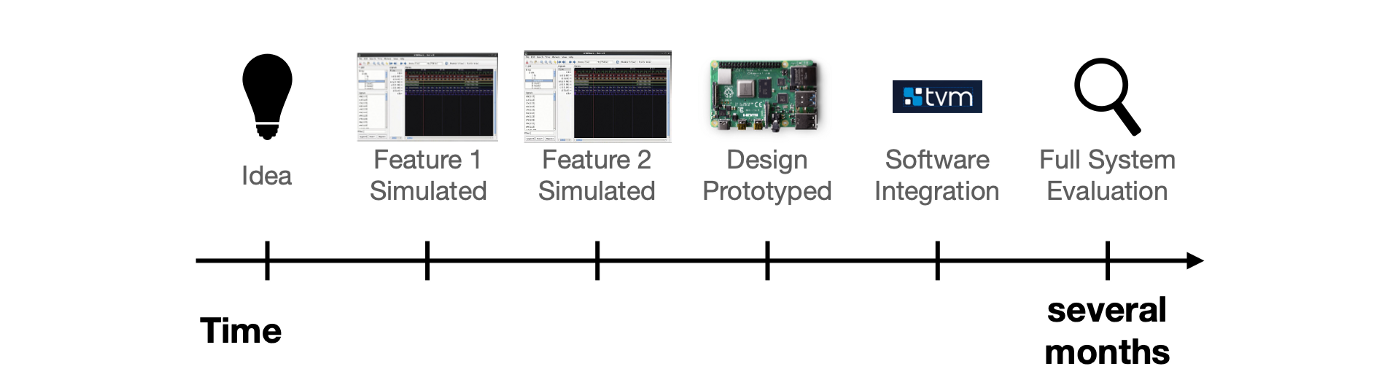
Typical hardware development is slow and doesn’t leave much room for error.
Unfortunately, the evaluation of a complete hardware-software ML stack is prohibitively expensive, both in terms of time and engineering. We strongly believe that we can reduce the cost of this evaluation by integrating hardware designs to TVM at the beginning of the hardware development process. Additionally, we believe that developers should be able to assess the benefits of hardware optimizations on complete ML workloads, rather than low-level hardware tests. Therefore, a more productive design timeline is possible using this more agile process:
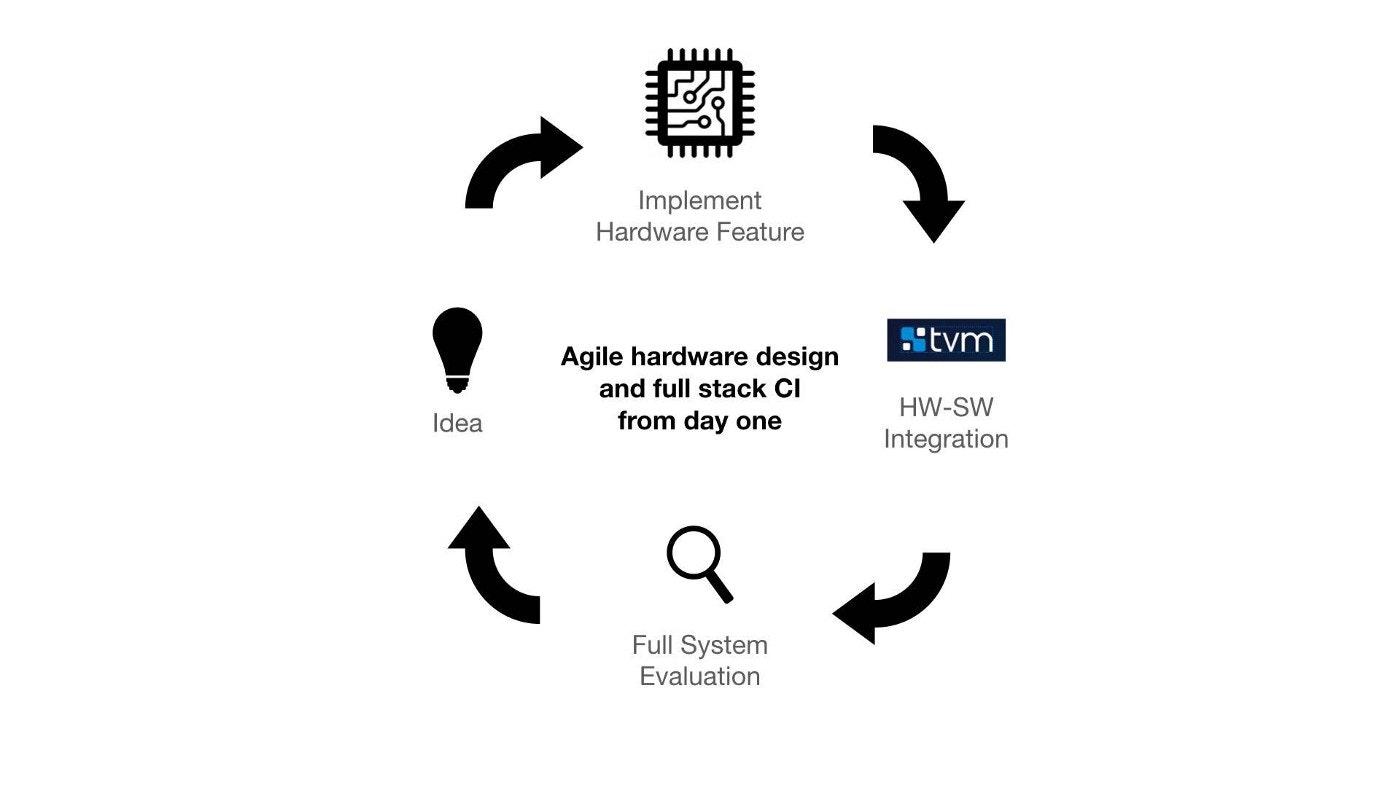
From day one, hardware simulation is driven by TVM on complete ML workloads. This accelerates the system design iteration loop.
With this approach, the entire system is evaluated every time a new hardware feature is added until the device is manufactured. Additionally, hardware and compiler support can be built incrementally, benefiting developers with continuous integration (CI) of a complete system stack.
Our approach: Bring your own RTL (ByoRTL)
Building hardware and software integration requires a mechanism for language interoperability. ML accelerators are described using either software languages (C/C++ or OpenCL) or hardware languages (Chisel or Verilog). Regardless of the source language, most of these implementations are translated down to Verilog. Additionally, current open-source hardware simulators like Verilator compile Verilog implementations down to C++ libraries to simulate the hardware on conventional machines. The hardware-software integration we propose in TVM uses Verilator to generate simulation libraries that can be driven by the rest of the TVM stack via foreign interfaces (CFFI).
Concretely, we introduce an interaction layer between TVM and the hardware design under development. Once the hardware is implemented on an FPGA or manufactured as an ASIC, the interaction layer can remain unchanged. It’s worth noting that the implementation of this interface is left to the user, providing flexibility on how the hardware design interoperates with TVM. The following is the important subset of this device interface:
/* allocate Verilator object */
extern "C" TVM_DLL VerilatorHandle VerilatorAlloc();
/* deallocate Verilator object */
extern "C" TVM_DLL void VerilatorDealloc(VerilatorHandle handle);
/* read Verilator register or memory */
extern "C" TVM_DLL int VerilatorRead(VerilatorHandle handle, int id, int addr);
/* write Verilator register or memory */
extern "C" TVM_DLL void VerilatorWrite(VerilatorHandle handle, int id, int addr, int value);
/* reset Verilator for n clock cycles */
extern "C" TVM_DLL void VerilatorReset(VerilatorHandle handle, int n);
/* run Verilator for n clock cycles */
extern "C" TVM_DLL void VerilatorRun(VerilatorHandle handle, int n);In addition to the device interface, we added an opaque kernel library that lets users define how operators are implemented according to the hardware capabilities available. For example, one can decompose the TVM’s add operator into simple scalar-addition operations implemented in Verilog and use the device interface to drive hardware as:
extern "C" void verilator_add(VerilatorHandle handle, int *data, int *weight, int *out, int p_h_, int p_w_) {
for (int64_t i = 0; i < p_h_; ++i) {
for (int64_t j = 0; j < p_w_; ++j) {
int64_t k = i * p_w_ + j;
VerilatorWrite(handle, 0, 0, data[k]);
VerilatorWrite(handle, 1, 0, weight[k]);
VerilatorRun(handle, 1);
out[k] = VerilatorRead(handle, 2, 0);
}
}
}Additionally, we extended the code generation and runtime support in TVM to support arbitrary hardware, so operators and subgraphs from ML workloads can be selectively offloaded to the target design. For example, one could easily offload the above operator (add) from a Relay module using the following utility function in Python:
def offload(mod):
backend = "verilator"
mod = transform.AnnotateTarget([backend])(mod)
mod = transform.PartitionGraph()(mod)
return mod Show me the code
If you’re interested in trying out this introductory example to TVM’s ByoRTL, try the following hardware integration example in TVM. Below are additional pointers to the sources of this simple yet complete example:
Related Posts

Apache TVM democratizes efficient machine learning with a unified software foundation. OctoML is building an MLops automation platform on top of it.


As AI models get larger, the importance of each weight for a typical inferencing decreases...


